The problem with monetarist’s view of inflation

The monetarist view of view of inflation, based on the Equation of Exchange, MV=PY, where M stands for money, and P for the price level, says that if we assume V and Y (respectively, velocity and output) are fixed, then a proportional increase in M leads to a proportional increase in P.

So, inflation (an increase in P) is “always and everywhere a monetary phenomenon,” as Milton Friedman famously claimed.

Long-run stability of the velocity, or the filpside of it, money demand, however, is not a empirically founded assumption.

The figure below, taken from “And Yet It Moves:Inflation and the Great Recession” by David Miles, Ugo Panizza, Ricardo Reis and Ángel Ubide, plots velocity since 1980 for the three major countries and the Eurozone, and shows that velocity is highly volatile.

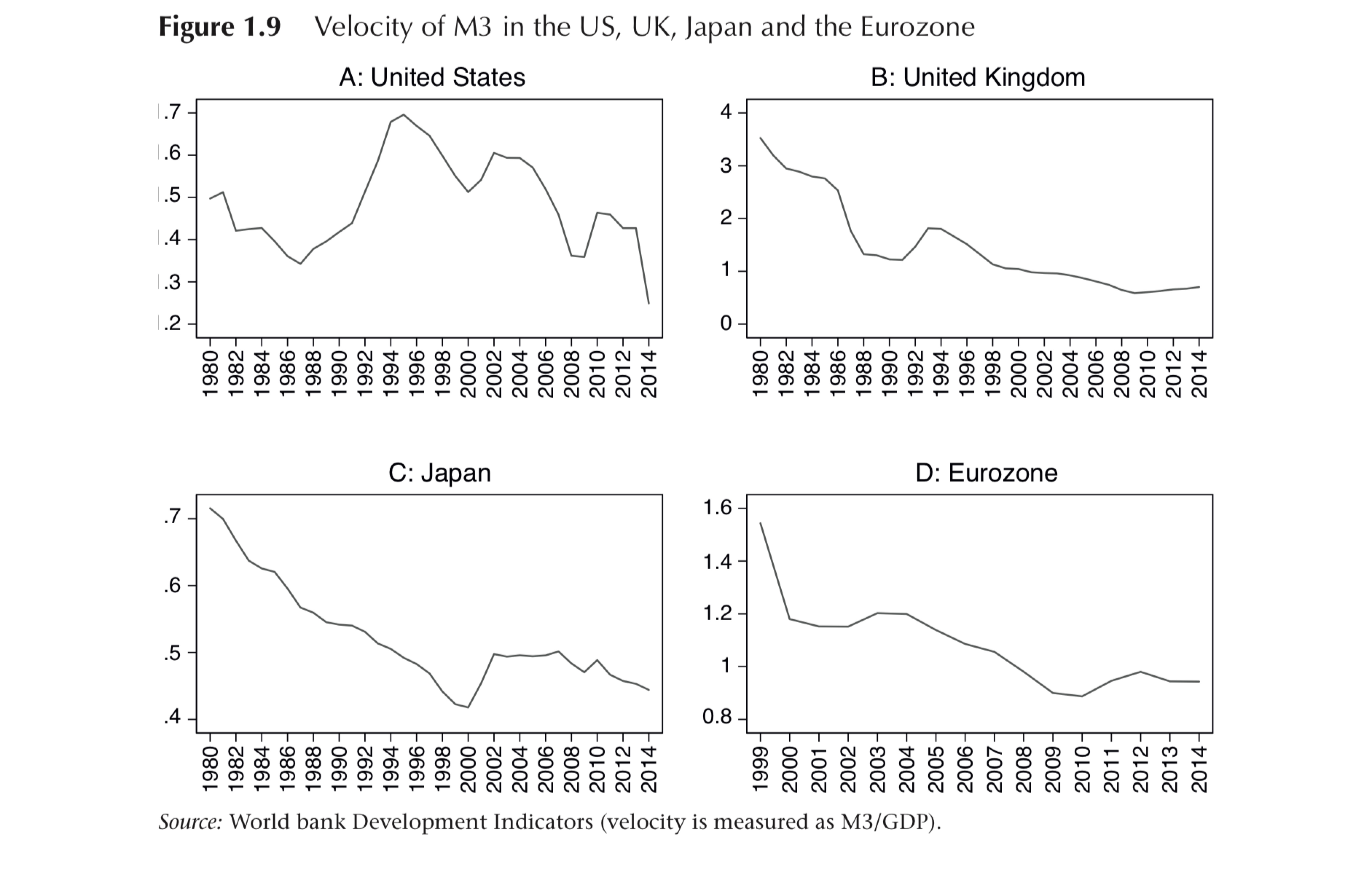
The authors added, “[m]ovements in P end up being dominated by unexplained movements in V rather than in M. Whenever central banks kept monetary aggregates steady as a policy, inflation ended up being quite volatile.”